A guide to Passive Membrane Properties
Menu
items in enquiry

    A guide to Passive Membrane Properties

    By Nour Al-muhtasib

    Special thanks to Dr. Garrett Neske and Dr. Carlos Aizenman

    Passive membrane properties allow neurons to conduct electrical impulses without the use of voltage-gated ion channels. They help us understand how the membrane potential changes in response to current across the cell membrane. The main ones are: input resistance, input capacitance, and axial resistance.

    Why are passive membrane properties important?

    Let’s take a pyramidal cell as an example. If it receives excitatory input at its apical dendrites, this influx of positive charge will generate a local change in voltage, which will travel down towards the soma. As it travels down, it becomes smaller.

    Passive membrane properties help us determine a few things:

    1. The size and magnitude of the voltage response.
    2. The time course of the voltage response (the shape of the voltage response).
    3. The distance the voltage response will travel.
    4. The speed of voltage response propagation (conduction velocity).

    Let’s review some basic concepts before we dive in

    Conductance (G, units of siemens (S)) is a measure of how easy it is for current to flow. Resistance (R, units of ohms (Ω)) is the measure of how difficult it is for current to flow: it is the inverse of conductance. Voltage (V) is the potential for charge to flow between two points, such as across a neuronal membrane. The cell can be modeled as a resistor-capacitor (RC) circuit, which is detailed in this article here. To summarise, it is a circuit that is made up of resistors and capacitors in parallel. The leak channels act as both resistors/conductors. The cell membrane acts as a capacitor which will be covered in detail later in this article.

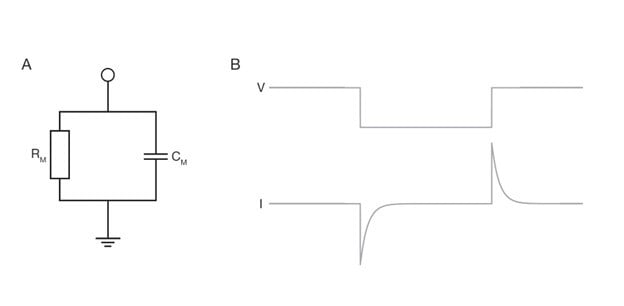
    Figure 1. Basic schematic of the electrical properties of a plasma membrane. A: A circuit diagram showing the membrane capacitance and membrane resistance in parallel to each other. B: Traces showing a command voltage step (top) and the resulting current response (bottom) for a simple plasma membrane being voltage clamped.
    Figure 1. Basic schematic of the electrical properties of a plasma membrane. A: A circuit diagram showing the membrane capacitance and membrane resistance in parallel to each other. B: Traces showing a command voltage step (top) and the resulting current response (bottom) for a simple plasma membrane being voltage clamped.

    Another important concept is Ohm’s law. It states that current (I, amperes (A)) through two points with a resistor (R) in between is directly proportional to voltage (V) across the two points. Mathematically it is written as I=V/R, better known as V=IR. When it comes to biological membranes, current flowing through channels is proportional to the voltage across the membrane. Therefore, for a passive membrane, there is a linear relationship between current and voltage.

    In a typical experiment you are recording from a soma, or cell body, so we are going to walk through passive membrane properties as they relate to the soma first and then how they relate to the distal dendrites and axons.

    Input Resistance

    Input resistance determines how much the cell depolarizes in response to a steady current. It is the total resistance of the cell. Due to Ohm’s law (V=IR), voltage response is proportional to resistance. Therefore, if two cells are receiving the same current input, the neuron with the larger input resistance, will have the larger voltage response. Input resistance is more relevant at the soma than at the distal dendrites.

    Input resistance depends on the total number of open ion channels on a neuron’s membrane and the size of the cell. The total number of channels depends on a parameter known as specific membrane resistance (Rm, Ω·cm2), and the size of the cell. Specific membrane resistance is dependent on the density of open channels. It is the membrane’s ability to pass current per unit membrane area, therefore you are only looking at segment of the neuron.

    Hint: It has always helped me to think of input resistance as the entire pizza and specific membrane resistance as a slice of the pizza.

    Note: Specific membrane resistance is derived from specific membrane conductance, which is given in units of S/cm2. Since resistance is the inverse of conductance, the units for specific membrane resistance are Ω·cm2.

    So now what happens to input resistance?

    We get this equation: Rin = Rm /Area(membrane)

    Therefore:

    1. As Rm decreases (more open channels, more leakiness), input resistance decreases
    2. As the size of the cell increases (the assumption is there are more channels), input resistance decreases

    To summarise: for synaptic input to the soma, a cell with increased input resistance will have an increased voltage response.

    Input Capacitance

    Have you ever walked into a room and turned on the switched and it has taken just a bit for the lights to turn on? A similar thing happens with a cell, for very similar reasons. The change in voltage after current insertion is not instantaneous. The current pulse is a square one and the change in voltage is a curve. There is a delay in voltage response because the lipid bilayer acts as a capacitor which stores charge in a circuit.

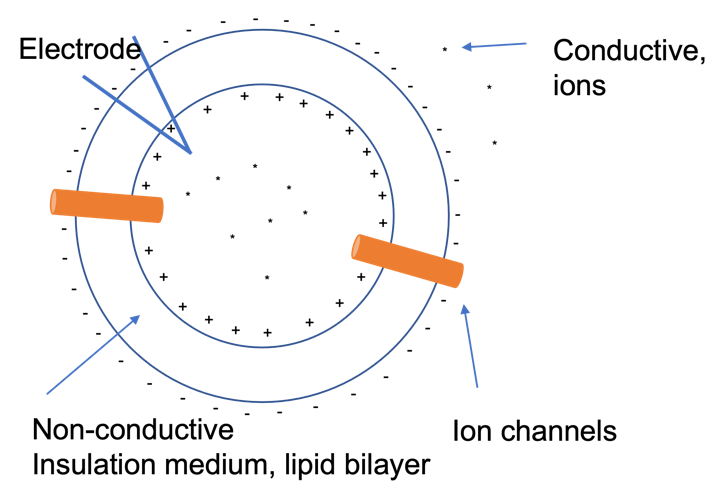
    Figure 2: A hypothetical cell with a lipid bilayer that is nonconductive
    Figure 2: A hypothetical cell with a lipid bilayer that is nonconductive

    Note: The image is representing relative charges.

    Let’s take the hypothetical cell in Figure 2 as an example. It has lipid bilayer that is nonconductive because ion cannot pass through it because everything is packed very tightly. The inside of the cell consists of a variety of material including conductive materials such as ions. There are also more ions, which are conductive material extracellularly. When doing an electrophysiology experiment you have an electrode which will insert a depolarizing current. Before it can depolarize the neuron completely it must charge the capacitor, which consists of storing positive charges on the inside of the membrane which will attract negative charges extracellularly. This causes a delay in the voltage response.

    The total capacitance of a neuron is called the input capacitance. It is derived from two factors: specific membrane capacitance, Cm, and the size of the cell. This brings us to this formula: Cin = CmArea(membrane)

    Unlike input resistance, input capacitance is proportional to cell size. The bigger the cell, the higher the input capacitance.

    What does capacitance depend on?

    1. Surface area of the cell
      1. Increases with the surface area of the cell
      2. The cell has a greater capacity to store
    2. Distance between the bilayer
      1. Decreases with distance between the bilayer because there is a greater separation of charge
      2. The positive charges being stored intracellularly have a harder time attracting the negative extracellular charges
    3. Insulation medium (composition of the bilayer)
      1. Typically does not change, therefore not a major contributing factor to cell-to-cell variation

      How does input capacitance affect the time course of the response? A smaller input capacitance leads to a faster time course.

      Time Constant

      Taken together, input resistance and input capacitance give us a parameter called the time constant (𝛕), it is the product of RinCin. It is the time it takes the membrane potential to reach to (1 – 1/e), where e is equal to around 2.72. This is equal to ~63% of the steady state value. Conversely, it is the time it takes to fall to ~37% of its steady state value. A short time constant means shorter rise time. A long time constant means slow rise time.

      If a cell only had resistive properties, the voltage response would be a square pulse. If it only had capacitive properties, the voltage response would be linear (but in reality, nothing would happen because there would be no path for current to flow). However, since the membrane is essentially a resistor and capacitor in parallel, that is why the voltage response is a curve.

      As a reminder, Rin = Rm /Area(membrane) and Cin = CmArea(membrane), therefore time constant is also equal to RmCm.

      Therefore, although a bigger cell would be less resistive, it would also be more capacitive.

      Axial resistance

      So far, we have been talking about how the passive membrane properties affect the voltage response in the soma, but how about spatially extended parts of the neurons, such as distal dendrites or axon? There are a few dendritic properties that become important. To derive the important properties, a process is taken and broken into segments and we get RC circuits. They consist of: membrane resistance rm, membrane capacitance cm, and axial resistance ra.

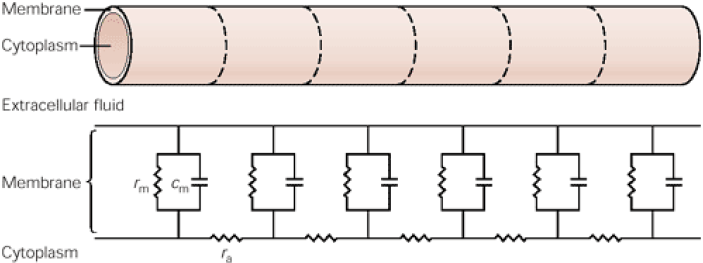
      Figure 3: A neuronal process can be represented by an electrical equivalent circuit. The process is divided into unit lengths. Each unit length of the process if a circuit with its own membrane resistance and capacitance. All the circuits are connected by resistors, which represent the axial resistance of segments of cytoplasm, and a short circuit, which represents the extracellular field. Koester, J. (2021). Membrane Potential. In S. Siegelbaum, E. R. Kandel, S. H. Mack, & J. Koester (Eds.), Principles of Neural Sciences (6th ed., pp. 142–149). Book Chapter, McGraw-Hill Professional Publishing.
      Figure 3: A neuronal process can be represented by an electrical equivalent circuit. The process is divided into unit lengths. Each unit length of the process if a circuit with its own membrane resistance and capacitance. All the circuits are connected by resistors, which represent the axial resistance of segments of cytoplasm, and a short circuit, which represents the extracellular field. Koester, J. (2021). Membrane Potential. In S. Siegelbaum, E. R. Kandel, S. H. Mack, & J. Koester (Eds.), Principles of Neural Sciences (6th ed., pp. 142–149). Book Chapter, McGraw-Hill Professional Publishing.


      Membrane resistance, rm (this is lower case rm) is an indication of how much current leaks out of the cell from the process. The formula for rm is Rm/2πr. A bigger process will have a greater radius and therefore a smaller rm. Membrane resistance, rm, will dictate the size and magnitude of the voltage response in the distal dendrites.

      Membrane capacitance, cm is the capacitance per unit length. The units are F/cm. A smaller membrane capacitance means a faster voltage response time course.

      Axial resistance is the resistance inside of the cell. The formula for axial resistance is ra= ρ/ πr2. ρ is the specific resistance of the cytoplasm Ω*cm. πr2 is the cross-sectional area. Therefore, as the cross-section of the process gets bigger the axial resistance gets smaller.

      Taken together, axial resistance and membrane resistance help us determine a property known as the length constant, termed by λ. The length constant determines how far the voltage response will travel.

      λ = √rm/ra

      A longer length constant means the voltage response will travel further down the process. What if we are comparing a small process and big process? The process will have a longer length constant because as the radius increases, ra decreases faster than rm.

      Myelination decreases membrane leak and will increase rm and therefore increase the length constant. Thus, allowing voltage response to travel faster along myelinated segments of axons.

      Conduction velocity is the speed at which an action potential propagates down the process. It is inversely proportional to the product of racm.

      What are ways to increase conduction velocity?

      • Decrease ra via increased diameter
      • Decrease cm = myelination

      In Summary

      Passive membrane properties help us determine a few things:

      1. The size and magnitude of the voltage response.
        1. For distal dendrites: Larger membrane resistance = larger voltage response
        2. For the soma: Larger input resistance = larger voltage response
      2. The time course of the voltage response.
        1. For distal dendrites: smaller cm = faster timer course
        2. Smaller input capacitance = faster timer course
      3. The distance the voltage response will travel.
        1. A longer length constant = the voltage response will travel longer.
      4. The speed of voltage response propagation (conduction velocity).
        1. Increases with increased process diameter and myelination

      About the Author

      Nour is a postdoc at Yale University in New Haven, CT. Her work focuses on cue-induced relapse of cocaine addiction. Other topics she is passionate about include science communication, education, and inclusion. You can find her on twitter at @Nouronal.

      Want to learn more?

      Sign up to our news bulletin to receive the latest advice guides, news and product updates. All content is focused around giving you the tools to achieve ground-breaking findings.

      Other articles you may be interested in

      Contact Form

      Contact us

      * denotes required field

      Select your interests